2157.
Cəm
Romanın valideynləri ona n
sayda təpəsi və n – 1 sayda
tilləri olan istiqamətlənməmiş əlaqəli
çəkili qraf hədiyyə edirlər. Roman qrafda olan
bütün yolların ümumi uzunluğunu tapmaq istəyir.
Yolun uzunluğu onda olan tillərin uzunluqlarının
cəmidir. Roman hesab edir ki, u-dan v-yə olan yol v-dən
u-ya
olan yol kimidir, buna görə də o onları
fərqləndirmir.
Giriş
verilənləri. İlk
sətir qrafda olan təpələrin n (2
≤ n ≤ 105) sayını ehtiva edir. Növbəti
n – 1 sətir qrafın tillərini təsvir edir. Hər
sətir üç tam ədəd ehtiva edir: Tilin birləşdirdiyi
təpələrin nömrələri (təpələr 1-dən n-ə qədər
nömrələnib) və tilin çəkisi.
Çıxış
verilənləri. Bütün
yolların uzunluqlarının cəmini 109 moduluna görə
hesablayın.
|
Giriş nümunəsi |
Çıxış
nümunəsi |
|
3 1 2 1 1 3 3 |
8 |
Məsələnin izahı. Qrafda
olan bütün yollar: 1 → 2, 1 → 3, 2 → 1 → 3, onların
uzunluqlarının cəmi 1 + 3 + 4 = 8.
Həll
verilənlər
strukturu - ağac
Alqoritmin
analizi
Ağacın
hər hansı bir təpəsindən dərininə axtarış
alqoritmini başladırıq. Ağacın w çəkili (u, v) tilini nəzərdən
keçirək. Tutaq ki v kökü
olan altağacın təpələrinin sayı c-yə bərabərdir. O zaman ağacda
tilin bir tərəfində olan təpələrin sayı c, digər tərəfində olan
təpələrinin sayı isə n – c olur. (u, v)
tili c * (n
– c) fərqli
yollara daxildir. Ona görə də bu tilin bütün yolların
uzunluqlarının cəminə əlavə edilməsi c * (n
– c) * w edir. Qalır dərininə axtarış alqoritmi ilə bütün
tilləri götürmək və onların əlavəsini
uzunluqların ümumi cəmi ilə cəmləmək
qalır.
Nümunə
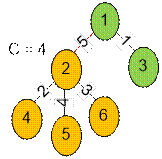
Çəkisi 5 olan (1,2) tilinin bütün
yolların ümumi uzunluqlarının cəminə əlavə
edilməsinə baxaq. Kökü 2 olan altağacın təpələrinin
sayı (2 təpəsini də nəzərə almaqla) c = 4-ə bərabərdir. O zaman
(1,2) kənarının o biri tərəfində n – c
= 6 – 4 = 2 təpə vardır. Beləliklə (1,2) təpələrini
birləşdirən müxtəlif yolların sayı c * (n
– c) = 4 * 2 = 8-ə bərabərdir.
Həqiqətən də belə yollar aşağıdakılardır:
1 – 2, 1 – 2 – 4, 1 – 2 – 5, 1 – 2 – 6,
3 – 1 – 2, 3 – 1 – 2 – 4, 3 – 1 – 2 – 5, 3 – 1 – 2 – 6
Çəkisi
5 olan (1,2) tillərinin bütün yolların uzunluqlarının
cəminə əlavə edilməsi c * (n – c) * w = 4 * 2 * 5 = 40 edir.
Alqoritmin
reallaşdırılması
Daxil edilmiş çəkili qrafı
g adlı əlaqəlilik siyahısında saxlayırıq.
#define MOD 1000000000;
vector<vector<pair<int,int> > > g;
v təpəsindən dərininə axtarış
alqoritmi. dfs funksiyası bizə kökü v (v daxil olmaqla) olan altağcın
təpələrinin sayını qaytarır. Təpələrin
hesablanması cnt dəyişənində
həyata keçirilir. v təpəsinin
altağaca daxil olduğunu hesab edərək başlanğıcda
cnt = 1 təyin edirik.
int dfs(int v, int
p = -1)
{
int
cnt = 1, c;
for(int i = 0; i < g[v].size(); i++)
{
int
to = g[v][i].first;
int
w = g[v][i].second;
Çəkisi
w olan (v, to) tilinə nəzər
salaq. Kökü to olan altağacda
təpələrin c sayını
hesablayırıq. (v, to) tili c * (n – c) müxtəlif yollara daxildir. Ona görə də o
tilin bütün yolların uzunluqlarının cəminə əlavə
edilməsi c * (n – c)
* w edir.
if (to != p)
{
c = dfs(to, v);
res = (res + 1LL * c * (n - c) *
w) % MOD;
cnt += c;
}
}
return
cnt;
}
Proqramın
əsas hissəsi. Çəkili qrafı g adlı əlaqəlilik
siyahısına oxuyuruq.
scanf("%d",&n);
g.resize(n+1);
for(i = 1; i < n; i++)
{
scanf("%d
%d %d",&u,&v,&d);
g[u].push_back(make_pair(v,d));
g[v].push_back(make_pair(u,d));
}
1 təpəsindən
dərininə axtarış alqoritmini başladırıq. Qrafın
təpələri 1-dən n-ə
gədər nömrələnir.
dfs(1);
Cavabı
çıxarırıq.
printf("%lld\n",res);
Java reallaşdırılması
import java.util.*;
import java.io.*;
class Edge
{
int to;
int weight;
public Edge(int to, int weight)
{
this.to = to;
this.weight = weight;
}
}
public class Main
{
static int MOD = 1000000000;
static ArrayList<Edge>[] g;
static int n, m;
static long res;
static int dfs(int v, int p)
{
int cnt = 1;
for(Edge edge : g[v])
{
int to = edge.to;
int w = edge.weight;
if (to != p)
{
int c = dfs(to, v);
res = (res + 1L * c * (n - c) * w) % MOD;
cnt += c;
}
}
return cnt;
}
public static void main(String[] args)
{
FastScanner con = new FastScanner(System.in);
n = con.nextInt();
g = new ArrayList[n+1]; // unchecked
for (int i = 0; i <= n; i++)
g[i] = new ArrayList<Edge>();
for (int i = 1; i < n; i++)
{
int u = con.nextInt();
int v = con.nextInt();
int d = con.nextInt();
g[u].add(new Edge(v,d));
g[v].add(new Edge(u,d));
}
dfs(1,-1);
System.out.println(res);
}
}
class FastScanner
{
BufferedReader br;
StringTokenizer st;
public FastScanner(InputStream inputStream)
{
br = new
BufferedReader(new InputStreamReader(inputStream));
st = new
StringTokenizer("");
}
public String next()
{
while (!st.hasMoreTokens())
{
try
{
st = new
StringTokenizer(br.readLine());
} catch (Exception e)
{
return null;
}
}
return st.nextToken();
}
public int nextInt()
{
return Integer.parseInt(next());
}
}
Python reallaşdırılması
MOD = 1000000000
def dfs(v, p = -1):
global res
cnt = 1
for to, w in g[v]:
if
to != p:
c = dfs(to, v)
res = (res + c * (n - c) * w) % MOD
cnt += c
return cnt
n = int(input())
g = [[] for _ in range(n + 1)]
res = 0
for _ in range(n - 1):
u, v, d = map(int, input().split())
g[u].append((v, d))
g[v].append((u, d))
dfs(1)
print(res)